Field Cycling Communication

Figure 1(a) T₁ dispersion for ¹H and ²H nuclei in H₂O and D₂O in porous glass, respectively, normalized to their bulk values. [1]

Figure 1(b) T1 dispersion for ¹H and ²H nuclei in H₂O and D₂O in bovine articular cartilage, respectively. [from unpublished data]

Ever since the early days of field-cycling NMR, the dynamics of molecules in the liquid or the solid state have been at the center of interest; even more, combination of both phases such as the motion of molecules on solid surfaces ask for the versatility of measuring the longitudinal relaxation time as a function of magnetic field strength. “Molecular dynamics” in this sense covers two different aspects: the statistics of rotational and translational motion of small molecules that are assumed as rigid, and the consequences of internal motion on the overall mobility in larger molecules such as polymers. Three examples shall highlight the power of field-cycling relaxometry for these dynamic studies:

Molecules on interfaces

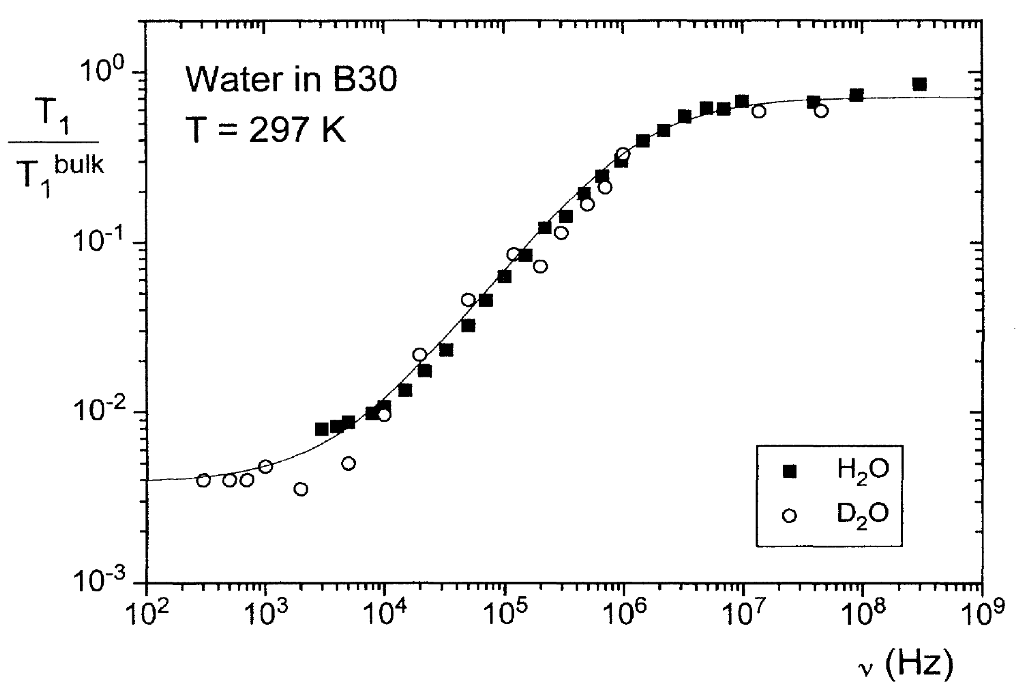
Porous Media have taken center stage of low-field relaxation studies, based on the huge commercial aspect of oil appraisal and recovery, and variable-field studies followed suit. Whereas relaxation of water and oil in rocks is complicated by the complexity of the natural substance, a number of problems in material science allow the use of simpler model materials that increase the chance of attributing a suitable model for molecular dynamics – or, more precisely, the way these dynamics are reflected in the relaxation properties. Validation of models require the use of field-cycling, preferentially over a range of frequencies as wide as possible. In essence, two main approaches have been followed since the 1990: Rainer Kimmich’s model [1,2] entirely relates on Reorientations Mediated by Translational Displacements (RMTD), i.e. molecules assume a preferential orientation on the solid interface and are reoriented while moving along its curvature, thus encoding the curvature into the relaxation dispersion function. This model was shown to be successful for “clean” surfaces with negligible amounts of impurities. A partial proof of the theory is in the observation that protons and deuterons show identical relaxation dispersion despite their different coupling mechanisms, making sure that interactions with neighboring molecules or surface sites is negligible. This has been observed for water in porous glass and, more recently, in biological tissue.

Figure 2(a) Dependence of 1H longitudinal relaxation times on Larmor frequency and temperature for the Ionic Liquid 1-butyl-3-methylimidazolium bromide. [5]

Figure 2(b) temperature dependence of the diffusion coefficient of this IL as obtained by pulsed field gradient (PFG) diffusometry and two different computations from the dispersion data in Figure 2(a). [5] Figure 3 Relaxation rates of ¹H and ¹⁹F nuclei in the ionic liquid 1-ethyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide with and without radicals.

The second approach presented by Jean-Pierre Korb [3,4] has the dominating contribution to relaxation in dipolar interactions with surface electrons such as iron and manganese centers, and it was successfully describing water and oil relaxation in rocks and cement. Common to all these approaches is the indirect detection of molecular reorientations on scales of nm to hundreds of nanometers, while longer distances are covered by conventional field gradient diffusometry experiments.

Ionic liquids

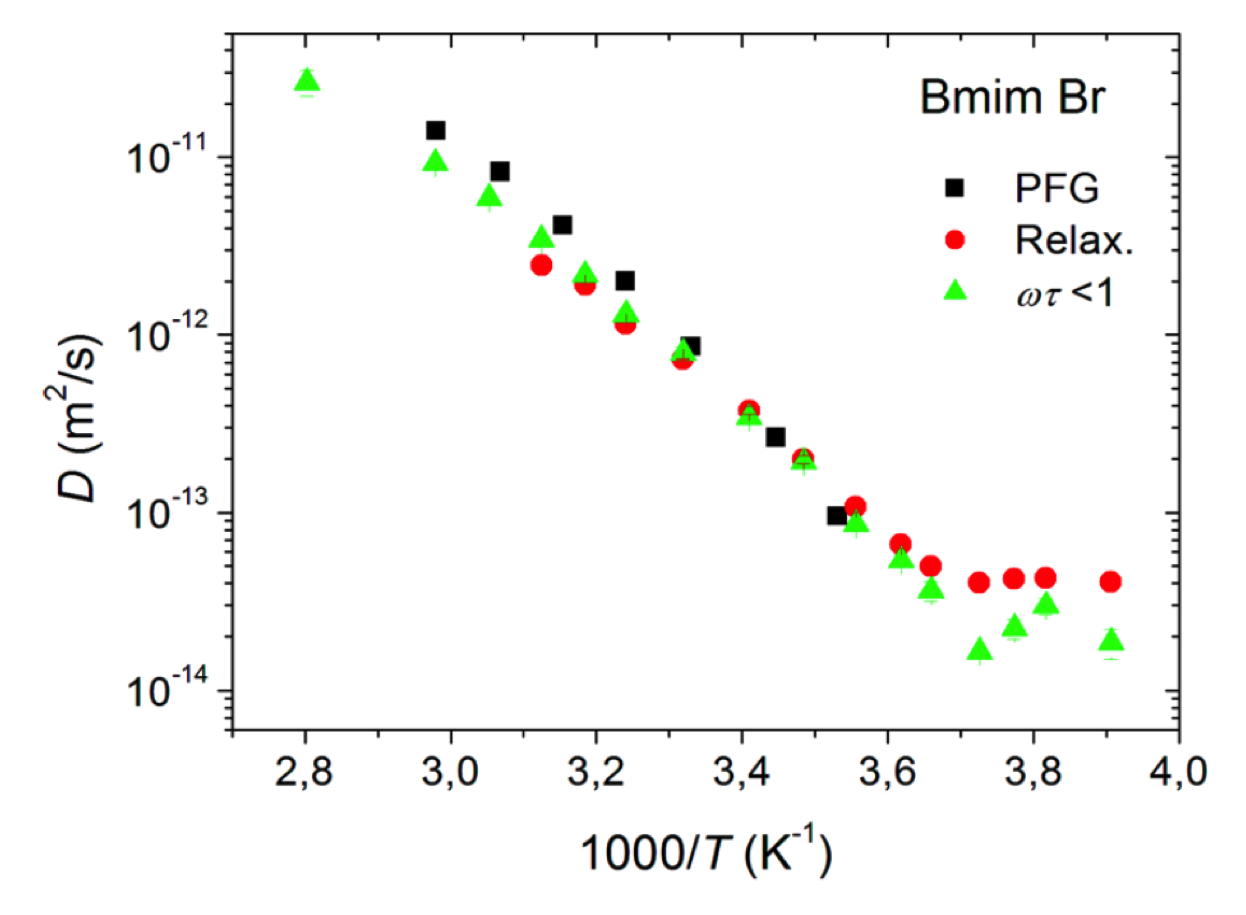
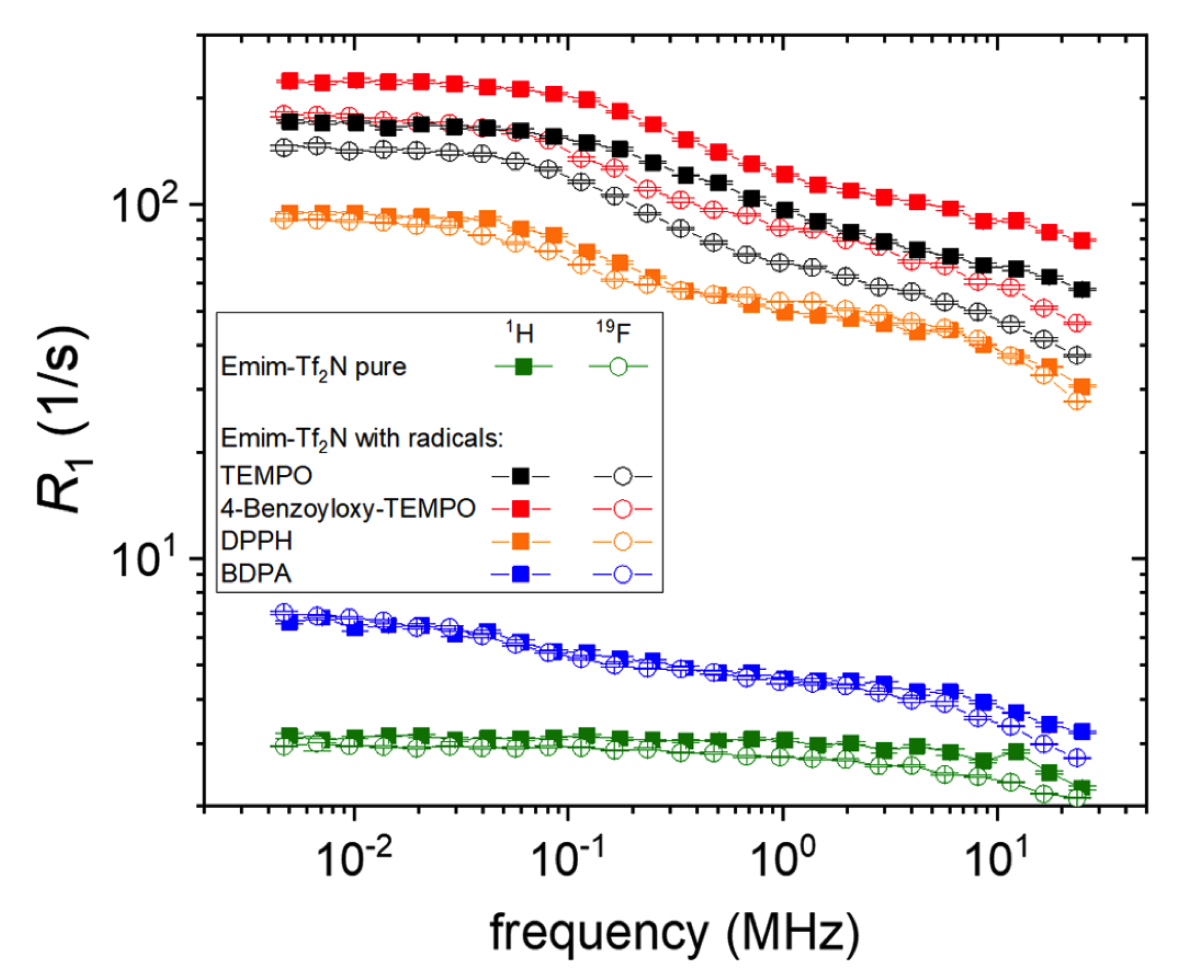
Molten salts with a melting point below 100°C are called ionic liquids (IL); their low melting point is a consequence of the rather low charge density of the ions. As in surface-interacting liquids, many ions can be considered rigid, and the main interest lies in the relative dynamics of anions and cations, their aggregation, and the consequences of their mobility for macroscopic transport and conductivity. More involved research may include the interaction with further molecules such as water or additional ions, as in lithium battery applications, or the effect of solid interfaces, charged and uncharged, on the ionic liquid. Many of these materials have been found to behave rather “harmless” and similar to viscous fluids, so that relaxation dispersion of both ions could be described by well-defined functions of rotational and translational motions modulating dipolar as well as scalar interactions. In the supercooled state, however, significant deviations were identified that were interpreted by the formation of intermittent clusters with a short lifetime that maintained the overall mobility and conductivity of the IL. More recently, the addition of stable radicals and the analysis of Dynamic Nuclear Polarization (DNP) combined with field-cycling relaxometry has helped to scrutinize the different contributions to the molecular dynamics of several anion/cation pairs of potential interest to energy storage materials.

Polymer Melts

A particular issue of polymer dynamics is the exceptionally wide range of timescales that can be observed between strictly local motion (vibration, sidechain rotation, small-scale reorientation) and global motion (center-of-mass diffusion); these can easily cover 12 orders of magnitude or more for long molecules with masses above 100 kDa in the melt. Theory for these timescales has been developed and has predominantly been described in the sense of mean-squared displacements (MSD) of individual atoms or segments within the chain; NMR relaxation does not directly measure MSD but it determines the spectrum of reorientations of segments which is related to that quantity. Since the 1980s is has been found that the dispersion of T₁ in polymers follows either logarithmic (short chains, solutions) or power-law (long chains, melts) dependences on Larmor frequency [7]. Even the wide range of field-cycling methods is not sufficient to cover the whole range of frequencies so that time-temperature superposition needs to be employed; however, it turns out that whenever a polymer is in the molten state, field-cycling covers the central part of the most “interesting” dynamic region between 10³ and 10⁸ s^-1; here, the data are most suitable to distinguish between the different existing models such as Rouse or reptation.

More recently, it has been clearly worked out that the original Doi/Edwards theory describes only the intramolecular interactions, whereas a strong intermolecular contribution of dipolarly coupled spins shows a different frequency dependence that is unique to NMR. By dilution of the samples in deuterated homologues, and by refinements of the corresponding models, it is now possible to isolate these two contributions and to describe motion in a wide range of frequencies successfully, allowing direct comparison to PFG diffusion methods, dielectric relaxation and neutron scattering to broaden the valid range of timescales of polymer dynamics even further [8,9].

Figure 4 (a) Master curves of T₁ for ¹H nuclei in undeuterated and partially deuterated polyisoprene melts of 287 kDa with apparent power laws indicated. (b) the same for ²H nuclei in methyl-deuterated polyisoprene. [10]

References